HB小咸鱼学习记录
因为疫情,大一在校半年便草草结束了,大二转眼将至。
疫情期间在家没事便抽空预习了预习大二要学的数据结构。
思来想去还是决定把学习的过程记录下来,方便自己以后查阅或者总结。
一点看法
在我看来,计算机的一大优势便是计算速度快。由此,人们在对某些问题的计算方面上,就不用像高斯找到1加到100的特殊技巧那样费力寻找技巧,直接依靠着计算机的计算力从1直接加到100就好。这种不需要技巧的运算方式就是暴力运算。而当你需要对图进行搜索的时候,最基础的就是暴力搜索。
就我目前的接触而言,常见的暴力搜索方式便是深度优先遍历与广度优先遍历了。
自我对于“深度优先搜索”的理解
dfs,字面来看就是以深度为优先的搜索方式。用通俗点来讲就是一条道走到黑。
就像我们规定以“前左右”的顺序走迷宫,而在寻找迷宫的出口时就可以看成进行了一次搜索。这样首先便是一直向前走下去。直到前面没有路了,我们就按照“前左右”再向左走,要是左边还走不通就再向右走直到走到死胡同里。当走到死胡同里的时候说明我们走完了一条迷宫的支线,此时我们可以认为自己单刀直入了这条支线的最深处。此时我们还需要找迷宫的出口,于是我们后退到上一个交叉路口的位置,按照“前左右”的顺序寻找一个没有进入过的支线。如果这个路口的支线已经全部走过,则再次后退到上一个交叉路口进行搜索 ……直到找到出口。
由此看来,如果运气好,我们第一次走便可能直接走到出口;但是运气差的话,可能把整个迷宫走完才能找到出口。
dfs的大致思路
首先,如上个片段所说,我们首先需要一个二维数组,来储存迷宫的大致情况,包括可以走的路、障碍物、入口、出口……
其次,我们对于已经走过的分叉路口要进行标记,防止进入已经进入过的路口,就像在走迷宫时你会主动避开走过的路线一样。这个通常用一个与上面地图大小相同的二维数组来储存坐标的状态。例如false代表没走过,true代表走过。
接着,我们需要对移动的规则进行规定。例如上文的例子规定的“上左右”,我们可以用一个二维数组来储存移动后坐标的变化:
1
| int direction[4][2] = {{0,-1},{-1,0},{1,0},{0,1}};
|
这个数组里面的四组数据就分别代表“上左右下”,在对坐标变换时进行
1
2
| int x1=x+direction[a][0];
int y1=y+direction[a][1];
|
即可实现对坐标的变化。且在变化后将x1,y1的点的状态进行更改,代表你已经来过这里了。
而当你到达死路进行后退且前往别的点的时候,记得把刚来过的点的状态进行更改,使下一次也能前往。
最后,我们需要进行判定,从而在找到出口时停止或者返回一些信息。
dfs的大致模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| void dfs(当前点位的信息)
{
if(到达中止条件)
{
执行一些东西;
return;
}
if(当前点位越界或者不符合规定)
return;
for(按照搜索的方向进行循环)
{
根据当前点位进行修改得到新点位;
if(新点位可以前往)
{
执行一些东西;
把新点位标记;
dfs(新点位的信息);
取消新点位的标记;
}
}
}
|
按照上面的思路大致可写以下代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| int map[100][100];
bool b_map[100][100];
int direction[4][2] = {{0,-1},{-1,0},{1,0},{0,1}};
int X,Y;
void dfs(int x,int y,int times)
{
if(x==X&&y==Y)
{
std::cout<<times<<"\n";
return;
}
for(int a=0;a<4;a++)
{
int x1=x+direction[a][0];
int y1=y+direction[a][1];
if(!map[x1][y1]&&!b_map[x1][y1])
{
b_map[x1][y1] = true;
dfs(x1,y1,time+1);
b_map[x1][y1] = false;
}
}
}
|
dfs的相关例题
dfs虽然搜索细致,但是在搜索过程中会进行大量的无意义运算,浪费时间,于是在运算中就要进行“剪枝”,即根据所求信息增加判定要求,从而最大限度的减少递归的调用次数,加快运算时间。
1.蓝桥杯 迷宫

OJ链接
思路: 在这道蓝桥杯的题目里,由于是求最短路径,所以用bfs来写比较简单。用dfs来写的话由于数据过大,不剪枝或者剪的不够的话稳稳的超时。
但是我们可以引入一个与图一样大小的二维数组,该数组用来储存到达该点的最小步数。则如果在递归中,当前步数大于当前点的最小步数,说明到达当前点多走歪路了,则中止递归。
在该条件的约束下,该dfs的运算效率得到了极大的提升。
AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include<bits/stdc++.h>
using namespace std;
#define X 30
#define Y 50
int a_map[31][51],ans=100000000,zhj=100000000;
bool b_map[31][51];
char fx[10000];
char t_fx[10000];
int z_4[4][2] = {{1,0},{0,-1},{0,1},{-1,0}};
char z[4] = {'D','L','R','U'};
int dp[31][51];
void dfs(int x,int y,int time,int he)
{
if(x==X&&y==Y)
{
if(time<zhj&&he<ans)
{
for(int now=0;now<time;now++)
fx[now]=t_fx[now];
zhj=time-1;
}
return;
}
for(int a=0;a<4;a++)
{
if(he+z[a]>ans)
continue;
int x1=x+z_4[a][0];
int y1=y+z_4[a][1];
if(x1<1 || y1<1 || x1>X || y1>Y)
continue;
if(b_map[x1][y1])
continue;
if(time+1>dp[x1][y1])
continue;
dp[x1][y1]=time+1;
b_map[x1][y1]=true;
t_fx[time] = z[a];
dfs(x1,y1,time+1,he+z[a]);
b_map[x1][y1]=false;
}
}
int main()
{
memset(fx,0,sizeof(fx));
memset(a_map,0,sizeof(a_map));
memset(b_map,false,sizeof(b_map));
memset(dp,999999,sizeof(dp));
for(int a=1;a<=X;a++)
{
for(int b=1;b<=Y;b++)
{
a_map[a][b] = getchar()-'0';
if(a_map[a][b]==1)
b_map[a][b]=true;
}
getchar();
}
b_map[1][1] = true;
dfs(1,1,0,0);
for(int now=0;now<=zhj;now++)
{
printf("%c",fx[now]);
}
return 0;
}
|
该思路原地址
2.蓝桥杯 全球变暖
题目
你有一张某海域NxN像素的照片,”.”表示海洋、”#”表示陆地,如下所示:

其中”上下左右”四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有2座岛屿。
由于全球变暖导致了海面上升,科学家预测未来几十年,岛屿边缘一个像素的范围会被海水淹没。
具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋),它就会被淹没。
例如上图中的海域未来会变成如下样子:
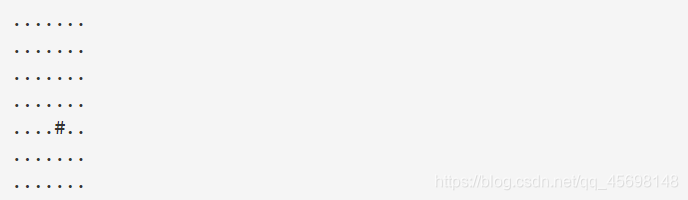
请你计算:依照科学家的预测,照片中有多少岛屿会被完全淹没。
输入
第一行包含一个整数N。 (1 <= N <= 1000)
以下N行N列代表一张海域照片。
照片保证第1行、第1列、第N行、第N列的像素都是海洋。
输出
一个整数表示答案。
样例输入

样例输出
1
OJ链接
思路:在接收初始图之后,首先搜索查找初始岛屿数,在找到一个岛屿后,对整个岛屿进行标记,防止重复计数。随后再次进行搜索,如果有四周均为陆地的坐标,则标记此坐标未被淹没。最后查找所有未被淹没的坐标,并将坐标所处的整个岛标记,防止重复计数。初始岛屿数量减去未被淹没岛的数量,即为被淹没的岛的数量。
AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
| #include <bits/stdc++.h>
using namespace std;
char maps[1001][1001];
void dfs1(int x,int y)
{
if(maps[x][y]!='#')
return;
maps[x][y]='1';
dfs1(x+1,y);
dfs1(x-1,y);
dfs1(x,y+1);
dfs1(x,y-1);
}
void dfs2(int x,int y)
{
if(maps[x][y]=='.')
return;
if(maps[x+1][y]=='1'&&maps[x-1][y]=='1'&&maps[x][y+1]=='1'&&maps[x][y-1]=='1')
{
maps[x][y]='2';
}
dfs1(x+1,y);
dfs1(x-1,y);
dfs1(x,y+1);
dfs1(x,y-1);
}
void dfs3(int x,int y)
{
if(maps[x][y]=='.')
return;
maps[x][y]='.';
dfs3(x+1,y);
dfs3(x-1,y);
dfs3(x,y+1);
dfs3(x,y-1);
}
int main()
{
int n,first_num=0,end_num=0;
scanf("%d",&n);
for(int a=1;a<=n;a++)
{
for(int b=1;b<=n;b++)
{
while(1)
{
scanf("%c",&maps[a][b]);
if(maps[a][b]=='.'||maps[a][b]=='#')
break;
}
}
}
for(int a=1;a<=n;a++)
{
for(int b=1;b<=n;b++)
{
if(maps[a][b]=='#')
{
dfs1(a,b);
first_num++;
}
}
}
for(int a=1;a<=n;a++)
{
for(int b=1;b<=n;b++)
{
if(maps[a][b]=='1')
{
dfs2(a,b);
}
}
}
for(int a=1;a<=n;a++)
{
for(int b=1;b<=n;b++)
{
if(maps[a][b]=='2')
{
dfs3(a,b);
end_num++;
}
}
}
cout<<first_num-end_num;
return 0;
}
|
3.leetcode 路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/path-sum OJ链接
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public:
bool hasPathSum(TreeNode* root, int sum)
{
kg=false;
if(root!=NULL)
dfs(root,root->val,sum);
return kg;
}
void dfs(TreeNode* root,int now,int end)
{
if(now==end&&root->left==NULL&&root->right==NULL)
{
kg = true;
return;
}
if(root->left==NULL&&root->right==NULL)
{
return;
}
if(root->left!=NULL)
dfs(root->left,now+root->left->val,end);
if(root->right!=NULL)
dfs(root->right,now+root->right->val,end);
}
private:
bool kg;
};
|
4.leetcode 路径总和II
给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
[
[5,4,11,2],
[5,8,4,5]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/path-sum-ii OJ链接
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
AC代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Solution {
public:
vector<vector<int>> pathSum(TreeNode* root, int sum)
{
if(root)
{
temp.push_back(root->val);
dfs(root,sum-root->val);
}
return ps;
}
private:
vector<vector<int>>ps;
vector<int>temp;
void dfs(TreeNode* root,int end)
{
if(end==0&&!root->left&&!root->right)
{
vector<int>t=temp;
ps.push_back(t);
return;
}
if(!root->left&&!root->right)
{
return;
}
if(root->left)
{
temp.push_back(root->left->val);
dfs(root->left,end-root->left->val);
temp.pop_back();
}
if(root->right)
{
temp.push_back(root->right->val);
dfs(root->right,end-root->right->val);
temp.pop_back();
}
}
};
|
小结
在使用dfs中,要根据题目数据选择合适的数据类型。
比如在题目数据过大时,申请较大的二维数组很容易失败。即使申请成功也会造成极大的内存浪费,循环时也很不方便。
这时就可以使用stl里的vector来储存数据,可以很好的提高的数据获取效率。
要尽量多的进行筛选,增加效率
好多题不止考的是dfs,甚至会考一点dp,所以要多想多做,寻找搜索中的共同点并对症下药。
dfs的常用环境
找最长路,特殊路等等等等。一般对带权图的搜索都用dfs。
在刷蓝桥杯的题的途中发现好多题都可以用dfs进行暴力,但是往往会超时。要想ac还得换题目想让你用的方法。但是往往能过几个检测点,所以不会的题都可以dfs一下混点分哈哈哈哈哈。
总之,还是得多刷题,多积累经验。



