2016 蓝桥杯 剪邮票 dfs

发表于 分类于 阅读次数： 本文字数： 569 阅读时长 ≈ 2 分钟

这是2016年蓝桥杯C语言省赛B组的第七题

题目：
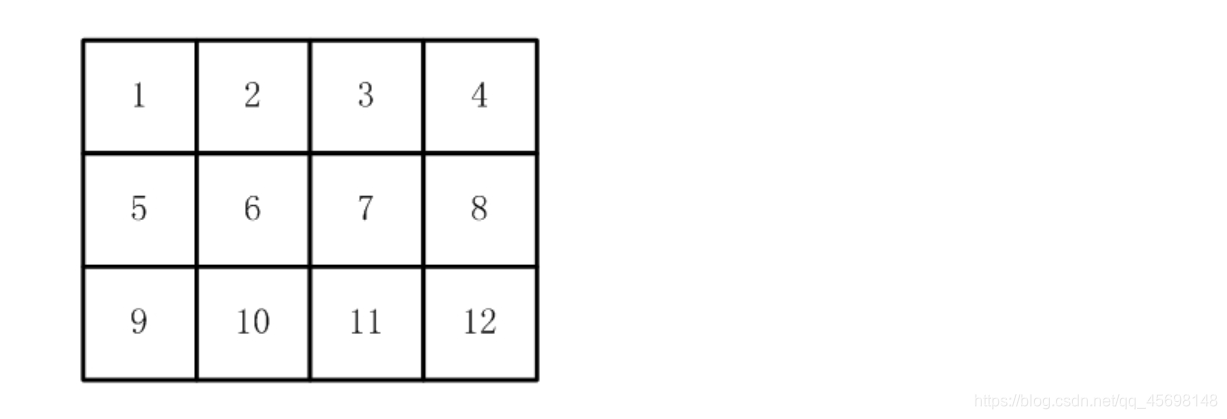
如下图, 有12张连在一起的12生肖的邮票。现在你要从中剪下5张来，要求必须是连着的。（仅仅连接一个角不算相连）
图1

比如，下面两张图中，粉红色所示部分就是合格的剪取。
图2

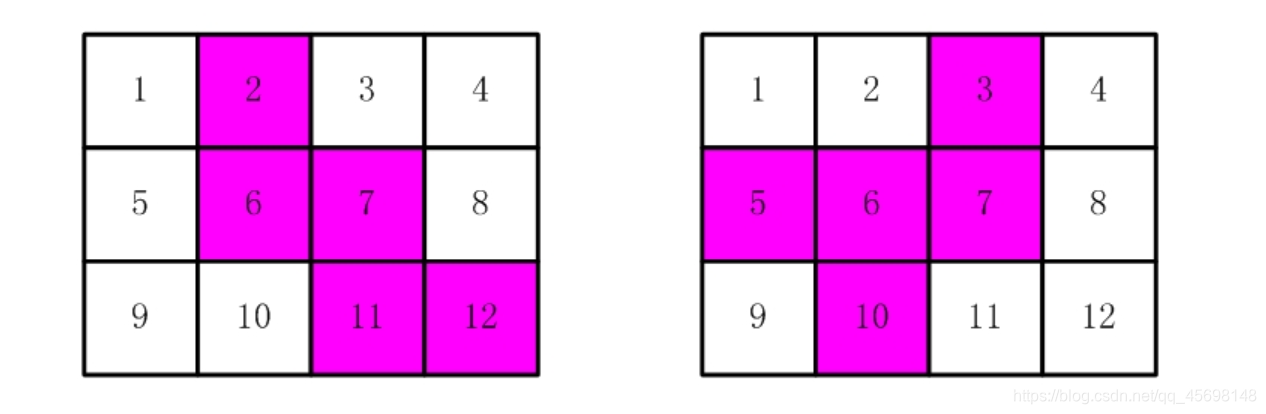
请你计算，一共有多少种不同的剪取方法。

输出：
请填写表示方案数目的整数。

OJ链接

思路：

  • 首先，我们将数组储存为
    1 2 3 4
    6 7 8 9
    11 12 13 14
    这样如果两数相减绝对值是5则是上下相邻关系，绝对值是1则是左右相邻关系。
  • 图3
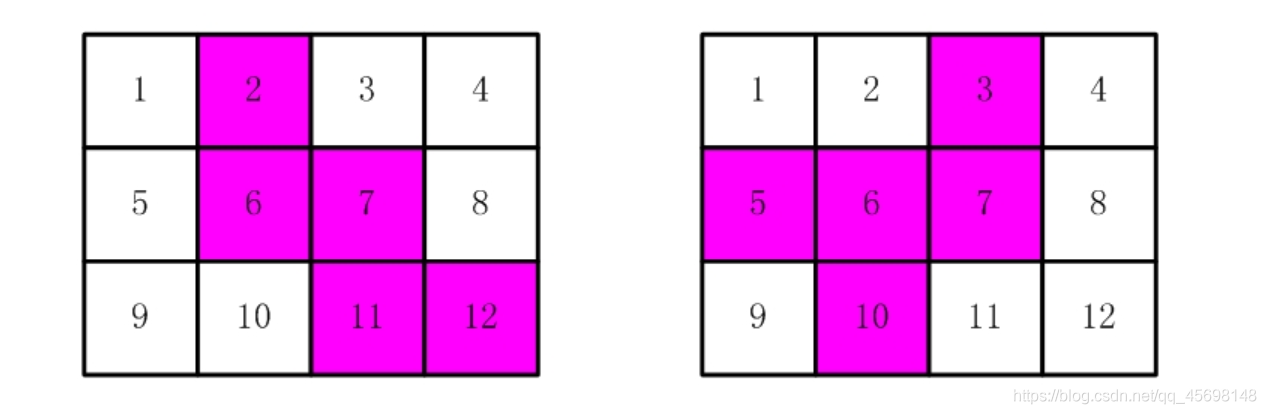
    通过对上图的观察我们可以发现，如果满足题意，则各邮票的相连邮票数量之和一定大于等于8，且每个邮票都有相连邮票。（上面两个图的相连数量之和都为8，如果剪12567的话相连数量就是9）按照这个规律我们就可以用双重循环来搜索答案了。
  • 前面用5层循环来组合出所有可能，防止重复。

AC代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include<bits/stdc++.h> 
using namespace std;

int temp[]={1,2,3,4,6,7,8,9,11,12,13,14};
int shuzu[5]; 
int ans=0;

/*
1  2  3  4
6  7  8  9
11 12 13 14
*/

bool judge()
{
	int count=0;
	for(int now=0;now<5;now++)//取前五个 看是否都相连 
	{
		int flag=0;//先假设不相连 
		for(int now1=0;now1<5;now1++)//挨个判断 
		{
			if(now==now1)
				continue;
			if(abs(shuzu[now1]-shuzu[now])==5||abs(shuzu[now1]-shuzu[now])==1)//上下相连 绝对值为5 或者 左右相连 绝对值为1 
			{
				flag+=1;//相连点位+1 
			}
		}
		if(flag==0)//如果是孤立点 没有相连点位 就直接返回false  
		{
			return false;
		}
		count+=flag;//加上连接数 
	}
	if(count<8)//如果连接数小于8 则说明5个点位没有相互相邻 
	{
		return false;
	}
	//printf("%d %d %d %d %d\n",shuzu[0],shuzu[1],shuzu[2],shuzu[3],shuzu[4]);
	return true;
}

int main()
{
	for(int a=0;a<12;a++)
	{
		for(int b=a+1;b<12;b++)
		{
			for(int c=b+1;c<12;c++)
			{
				for(int d=c+1;d<12;d++)
				{
					for(int e=d+1;e<12;e++)
					{
						shuzu[0]=temp[a],shuzu[1]=temp[b],shuzu[2]=temp[c],shuzu[3]=temp[d],shuzu[4]=temp[e];
						if(judge())
						{
							ans++;
						}
					}	
				}
			}
		}
	}
	cout<<ans; 
	return 0;
}