数据结构实操：STL标准红黑树(一)

发表于 分类于 阅读次数： 6 本文字数： 5.4k 阅读时长 ≈ 19 分钟
  • 之前一直在看侯捷大佬的《STL源码剖析》，透过标准库里的代码学到了许多。随后便想着按照STL标准来简单重写一个红黑树。当然，这里的简单是指对空间配置器结构的一些省略。
  • 代码部分本来在6月底就基本完成了，但是因为7月忙着吸收总结实习中学习的内容，所以一直搁置了红黑树的总结。由于《STL源码剖析》中并没有红黑树节点删除相关以及一些小细节的讲解，所以相关的内容是我在别的地方学习后根据STL标准自己补全的代码，如有纰漏，还请提醒。
  • 本次总结预计分为三篇，(一)中主要记录相关的代码思路结构，(二)中重点分析添加红黑树节点相关的内容，(三)中重点分析删除红黑树节点相关的内容。

零、我认为的STL标准

  首先，对于STL中的数据结构，不难发现它们除了自身的数据结构外还配套有空间配置器以及专属的迭代器。其中空间配置器中维护了一个内存池，符合标准的内存申请均从中获取；而迭代器则是为了更方便的对数据结构进行遍历，或是为了配合在之后STL中的算法模块。
  所以，我认为数据结构+空间配置器+专属迭代器=STL标准数据结构。但是由于篇幅有限，且我主要是为了学习红黑树相关的内容，所以在本文中对空间配置器进行了一些省略——直接进行new和delete操作。
  当然，STL里更直观的一个特点就是无数被typedef封装的详细(繁琐)的类型名，在下面的记录中，将会直观的展示它。

一、本文中红黑树的结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
总体分为三大块：
1.红黑树的空间配置器
2.红黑树的迭代器
3.红黑树数据结构相关

/* *** ***** *** */
其中红黑树的数据结构包括：
1.红黑树节点相关的定义
	1.1 红黑树节点颜色的定义(即红/黑)
	1.2 红黑数节点数据结构的定义(包括父/孩子节点、值、寻子节点最大/最小值函数)

2.红黑树相关的定义(围绕着红黑树节点)
	2.1 红黑树节点的创建、删除、获取(调用空间配置器)
	2.2 红黑树中获取节点内容(父/孩子节点、值等)的函数
	2.3 红黑树基础操作函数(插入、删除、寻找)
	2.4 一些基础的STL函数，例如begin()、end()、size()等等

3.红黑树的一些操作函数
	3.1 红黑树的左旋右旋操作函数
	3.2 红黑树的平衡性调整函数

/* *** ***** *** */
其中空间配置器包括：
1.空间配置器的基础定义
	1.1 分配内存
	1.2 释放内存

/* *** ***** *** */
其中迭代器包括：
1.迭代器的基础定义
	1.1 由于是双向迭代器，所以要有基础的前进和后退功能(++/--重载)
	1.2 要能实现提领和成员访问功能，所以要进行一些操作符重载

二、红黑树的数据结构

1. 红黑树的节点

1.1 节点颜色

  红黑树之所以叫做红黑树，是因为它的节点除了基础的值外，还具有颜色的属性，即红色和黑色。所以首先需要对红色和黑色进行定义：

1
2
3
4
//颜色类型定义
typedef bool _rb_tree_color_type;
const _rb_tree_color_type _rb_tree_red = false;//红色为0
const _rb_tree_color_type _rb_tree_black = true;//黑色为1

1.2 基础节点结构

  随后，我们对红黑树的基础单位——节点进行定义，其中节点数据结构中除了常规树节点里的左右孩子节点还需要有父节点以及颜色定义。其中，还需要声明两个函数，其作用是寻找到当前节点下最大和最小的孩子。由于红黑树是满足二叉排序树的特性的，所以最大子节点即为最右节点、最小子节点即为最左节点。定义如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//rb_tree 基础节点结构定义
struct _rb_tree_node_base
{
	typedef _rb_tree_color_type color_type;
	typedef _rb_tree_node_base* base_ptr;

	color_type color;//节点颜色
	base_ptr parent;//父亲
	base_ptr left;//左孩子
	base_ptr right;//右孩子

	//找孩子最小值
	static base_ptr minimum(base_ptr x)
	{
		while (x->left != 0)
		{
			x = x->left;
		}
		return x;
	}

	//找孩子最大值
	static base_ptr maximux(base_ptr x)
	{
		while (x->right != 0)
		{
			x = x->right;
		}
		return x;
	}
};

1.3 完整节点结构

  上面是对于基础节点的定义，但是很明显，其中并没有值。要声明值的话就需要用到泛型，而上面的基础定义不需要用到，由此可以进行分离。我感觉STL里很多东西都分离的很细，应该是为了逻辑和方便修改吧。再说到值，我们可以继承上面的base类型并引入泛型，创造出完整的红黑树节点数据结构：

1
2
3
4
5
6
7
//rb_tree 节点结构定义
template<class Value>
struct _rb_tree_node : public _rb_tree_node_base
{
	typedef _rb_tree_node<Value>* link_type;
	Value value_field;//节点值
};

  由此，一个完整的红黑树节点数据结构_rb_tree_node就被构造出来了，随后可以在节点的基础上，来构造红黑树以及它的相关操作函数。

2. 红黑树

2.1 构造思路

  由于前面已经构造出了红黑树的节点，那么可以像链表的数据结构一样，创建一个header头结点，这样就可以通过操作这个头结点来控制整个红黑树，这里先暂且不谈这个头结点里储存的内容(后面插入函数部分会说)。
  有了这个基础思路之后，我们就可以以该头结点为媒介和底层，定义各式各样的函数来操作或是获取以该头结点为根的红黑树中的内容。例如每个STL数据结构都有的begin()和end()，或是insert()和erase()等等非静态函数。然后是一些静态函数，方便获取传入节点的内容，毕竟对于用户而言，红黑树节点这个数据结构是被封装的，是不明的，所以需要一些静态函数来获取其中的内容。当然，也得有树/节点的构造/析构函数，这是建树的基础。

2.2 泛型内容

  在真正构造红黑树的数据结构前，还需要考虑的一个东西是其泛型的结构。那么都需要准备什么泛型呢？首先红黑树是二叉排序树，这就需要在插入中进行比较，所以需要引入键值对概念。由此这里就需要两种泛型，一个是key的泛型，一个是value的泛型。此外，前文对节点的定义中只存在值，所以需要有一个获取key的函数。对此，STL的做法是传入一个仿函数泛型来获取key。此外还需要传入一个比较函数(仿函数)来比较key，以及传入一个空间配置器泛型，所以标准的STL红黑树一共有五个泛型。但是，这里我省略了空间配置器泛型，来减少任务量，所以一共只有四个泛型，即键、值、取键函数、比较函数。

2.3 静态函数

  其中，我们需要定义一些构造函数，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
//以下六个函数获取节点x的成员
static link_type& left(link_type x)
{
	return (link_type&)(x->left);
}
static link_type& right(link_type x)
{
	return (link_type&)(x->right);
}
static link_type& parent(link_type x)
{
	return (link_type&)(x->parent);
}
static reference value(link_type x)
{
	return x->value_field;
}
static const Key& key(link_type x)
{
	return (key_type)KeyOfValue()(value(x));
}
static color_type& color(link_type x)
{
	return (color_type&)(x->color);
}
//以下六个函数获取节点x的成员
static link_type& left(base_ptr x)
{
	return (link_type&)(x->left);
}
static link_type& right(base_ptr x)
{
	return (link_type&)(x->right);
}
static link_type& parent(base_ptr x)
{
	return (link_type&)(x->parent);
}
static reference value(base_ptr x)
{
	return ((link_type)x)->value_field;
}
static const Key& key(base_ptr x)
{
	return (key_type)KeyOfValue()(value((link_type)x));
}
static color_type& color(base_ptr x)
{
	return (color_type&)((link_type)x->color);
}
//求极大值和极小值 节点基类方法已实现
static link_type minimum(link_type x)
{
	return (link_type)_rb_tree_node_base::minimum(x);
}
static link_type maximum(link_type x)
{
	return (link_type)_rb_tree_node_base::maximum(x);
}

  其中包含了基础的取父、孩子节点的函数和取键值、颜色的函数，使得使用者不需要直接操作节点结构，而是通过红黑树里封装好的link_type以及上面定义的这些函数来获取自己想要得到的内容。

2.4 树/节点的构造/析构函数

  首先，需要最基础的配置和释放空间的函数，这里通过调用空间配置器内的函数来完成操作，空间配置器的内容在下文。
  随后，是创建节点函数，在获取到空间后，调用其构造函数赋值。STL中也存在一个clone_node()来复制一个节点的颜色和值。
  最后就是销毁函数，不用多说什么了。这一部分具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
全局：
//构造函数调用
template<class T1, class T2>
inline void construct(T1* p, const T2& value)
{
	new (p) T1(value);
}

//析构函数调用
template<class T>
inline void destroy(T* pointer)
{
	pointer->~T();
}

红黑树内protected：
	link_type get_node()//获取节点(配置空间)
	{
		return rb_tree_node_allocator::allocate();
	}
	void put_node(link_type p)//释放节点(回收空间)
	{
		rb_tree_node_allocator::deallocate(p);
	}
	link_type create_node(const value_type& x)//创建节点
	{
		link_type temp = get_node();
		try
		{
			construct(&temp->value_field, x);
		}
		catch (const std::exception&)
		{
			put_node(temp);
		}
		return temp;
	}
	link_type clone_node(link_type x)//复制节点值与色
	{
		link_type temp = create_node(x->value_field);
		temp->color = x->color;
		temp->left = 0;
		temp->right = 0;
		return temp;
	}
	void destroy_node(link_type p)//销毁节点
	{
		destroy(&p->value_field);//析构内容
		put_node(p);//释放内存
	}

2.5 非静态函数思路

  总体来说就是一些服务于红黑树的函数，例如初始化、插入、移除、寻找等等。还有一些基础的empty()、size、begin()、end()等等，服务于后面的迭代器和STL的算法部分。插入和移除等后面会细说，其余的也没有什么说的必要，就略过了。

2.6 红黑树数据结构部分代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
//红黑树的定义与声明
template<class Key, class Value, class KeyOfValue, class Compare>
class rb_tree
{
protected://基础
	typedef void* void_pointer;
	typedef _rb_tree_node_base* base_ptr;
	typedef _rb_tree_node<Value> rb_tree_node;
	typedef _rb_tree_color_type color_type;
public://类型封装
	typedef Key key_type;
	typedef Value value_type;
	typedef value_type* pointer;
	typedef const value_type* const_pointer;
	typedef value_type& reference;
	typedef const value_type& const_reference;
	typedef rb_tree_node* link_type;
	typedef size_t size_type;
	//空间配置器
	typedef _rb_tree_node_allocator<Value> rb_tree_node_allocator;
protected://内存管理相关
	link_type get_node()//获取节点(配置空间)
	{
		return rb_tree_node_allocator::allocate();
	}
	void put_node(link_type p)//释放节点(回收空间)
	{
		rb_tree_node_allocator::deallocate(p);
	}
	link_type create_node(const value_type& x)//创建节点
	{
		link_type temp = get_node();
		try
		{
			construct(&temp->value_field, x);
		}
		catch (const std::exception&)
		{
			put_node(temp);
		}
		return temp;
	}
	link_type clone_node(link_type x)//复制节点值与色
	{
		link_type temp = create_node(x->value_field);
		temp->color = x->color;
		temp->left = 0;
		temp->right = 0;
		return temp;
	}
	void destroy_node(link_type p)//销毁节点
	{
		destroy(&p->value_field);//析构内容
		put_node(p);//释放内存
	}
protected://基本数据与方法
	size_type node_count;//节点数量
	link_type header;//树根头 树根为parent 最小值为left 最大值为right
	Compare key_compare;//节点间键值比较准则
	//以下三个函数获取header的成员
	link_type& root() const
	{
		return (link_type&)header->parent;
	}
	link_type& leftmost() const
	{
		return (link_type&)header->left;
	}
	link_type& rightmost() const
	{
		return (link_type&)header->right;
	}
	//以下六个函数获取节点x的成员
	static link_type& left(link_type x)
	{
		return (link_type&)(x->left);
	}
	static link_type& right(link_type x)
	{
		return (link_type&)(x->right);
	}
	static link_type& parent(link_type x)
	{
		return (link_type&)(x->parent);
	}
	static reference value(link_type x)
	{
		return x->value_field;
	}
	static const Key& key(link_type x)
	{
		return (key_type)KeyOfValue()(value(x));
	}
	static color_type& color(link_type x)
	{
		return (color_type&)(x->color);
	}
	//以下六个函数获取节点x的成员
	static link_type& left(base_ptr x)
	{
		return (link_type&)(x->left);
	}
	static link_type& right(base_ptr x)
	{
		return (link_type&)(x->right);
	}
	static link_type& parent(base_ptr x)
	{
		return (link_type&)(x->parent);
	}
	static reference value(base_ptr x)
	{
		return ((link_type)x)->value_field;
	}
	static const Key& key(base_ptr x)
	{
		return (key_type)KeyOfValue()(value((link_type)x));
	}
	static color_type& color(base_ptr x)
	{
		return (color_type&)((link_type)x->color);
	}
	//求极大值和极小值 节点基类方法已实现
	static link_type minimum(link_type x)
	{
		return (link_type)_rb_tree_node_base::minimum(x);
	}
	static link_type maximum(link_type x)
	{
		return (link_type)_rb_tree_node_base::maximum(x);
	}
public://迭代器封装
	typedef _rb_tree_iterator<value_type, reference, pointer> iterator;
private://一些私有方法
	iterator _insert(base_ptr x_, base_ptr y_, const value_type& v);
	void _erase(link_type x);
	void init()//初始化header
	{
		header = get_node();//产生应该节点空间，令header指向它
		color(header) = _rb_tree_red;//header为红色 与root区分
		root() = 0;//root为空
		leftmost() = header;//令header的左子节点为自己
		rightmost() = header;//令header的右子节点为自己
	}
public://构造与析构
	rb_tree(const Compare& comp = Compare())
		: node_count(0), key_compare(comp)
	{
		init();
	}
	~rb_tree()
	{
		//clear();
		put_node(header);
	}
	rb_tree<Key, Value, KeyOfValue, Compare>& //重载=
		operator=(const rb_tree<Key, Value, KeyOfValue, Compare>& x);
public://STL的一些基础方法
	Compare Key_comp() const
	{
		return key_compare;
	}
	iterator begin()
	{
		return leftmost();
	}
	iterator end()
	{
		return header;
	}
	bool empty() const
	{
		return node_count == 0;
	}
	size_type size() const
	{
		return node_count;
	}
	size_type max_size() const
	{
		return size_type(-1);
	}
public:
	//不可重复插入
	std::pair<iterator, bool> insert_unique(const value_type& v);
	//可重复插入
	iterator insert_equal(const value_type& v);
	//删除-传入迭代器
	iterator erase(iterator x);
	//删除-传入值
	iterator erase(value_type& v);
	//寻找
	iterator find(const key_type& k);
};

3. 红黑树的操作函数

3.1 左旋函数

  首先这是一个全局函数，是用来调整树的平衡性的。红黑树相比普通树查找快的原因就是它是平衡二叉树，有着较平衡的查找次数，由此需要左旋以及右旋函数来调整平衡性；但它又没有AVL树那么严格的平衡要求，所以总体插入/查找效率达到最大化。
左旋
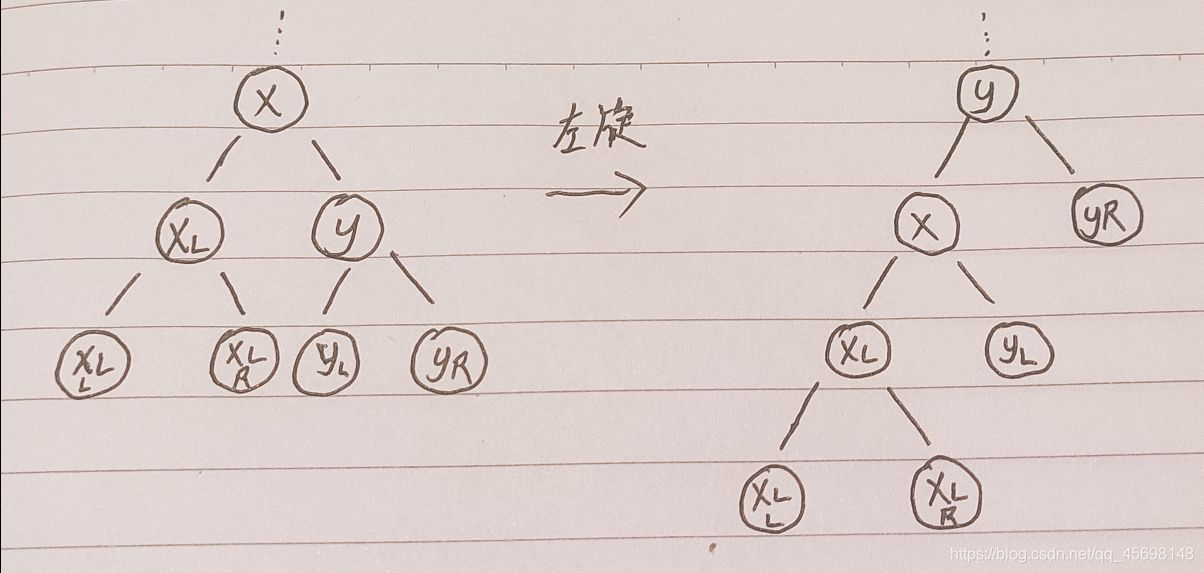
  左旋示意图如上，可以看到简而言之就是旋转点x变为其右子节点y的左子节点，随后y的左子节点变为x的右子节点。代码如下，其中需要注意边界条件以及父子关系的改变：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//rb_tree 左旋函数
inline void _rb_tree_rotate_left(_rb_tree_node_base* x, _rb_tree_node_base*& root)
{
	//printf("左旋\n");
	//x为旋转点，root为树根
	_rb_tree_node_base* y = x->right;//新建y为旋转点的右子节点
	x->right = y->left;//令x的右子节点为y的左子节点
	if (y->left != 0)//若y的左子树不为空
	{
		y->left->parent = x;//y的左子树的父亲改为x
	}
	y->parent = x->parent;//y的父亲改为x的父亲
	//令y顶替x的位置
	if (x == root)//当x为根
	{
		root = y;
	}
	else if (x == x->parent->left)//当x为parent的左子节点
	{
		x->parent->left = y;
	}
	else//当x为parent的左子节点
	{
		x->parent->right = y;
	}
	y->left = x;//x、y父子关系互换
	x->parent = y;
}

3.2 右旋函数

  总体来说右旋函数和左旋函数差不多，只是操作方法变了一些。总体就是旋转点x变为其左子节点y的右子节点，随后y的右子节点变为x的左子节点。右旋示意图以及相关代码如下，仍然需要注意边界条件以及父子关系的改变：
右旋

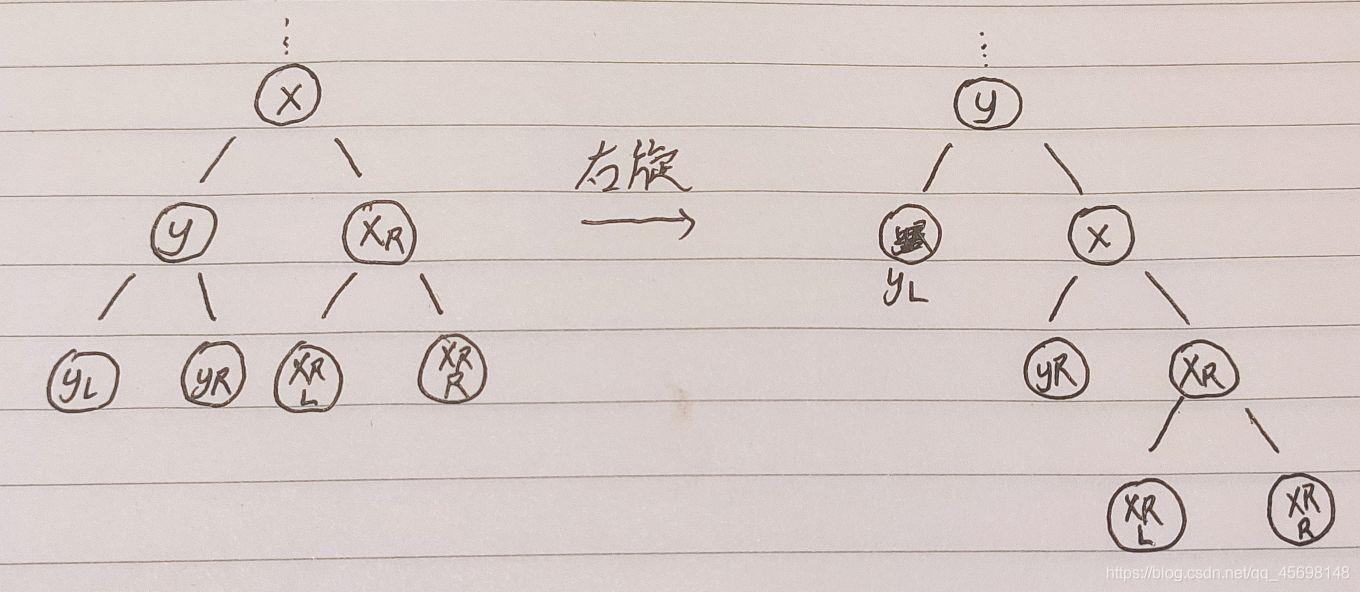
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//rb_tree 右旋函数
inline void _rb_tree_rotate_right(_rb_tree_node_base* x, _rb_tree_node_base*& root)
{
	//printf("右旋\n");
	//x为旋转点，root为树根
	_rb_tree_node_base* y = x->left;//新建y为旋转点的左子节点
	x->left = y->right;//令x的左子节点为y的右子节点
	if (y->right != 0)//若y的右子树不为空
	{
		y->right->parent = x;//y的右子树的父亲改为x
	}
	y->parent = x->parent;//y的父亲改为x的父亲
	if (x == root)//当x为根
	{
		root = y;
	}
	else if (x == x->parent->right)//当x为parent的右子节点
	{
		x->parent->right = y;
	}
	else//当x为parent的左子节点
	{
		x->parent->left = y;
	}
	y->right = x;//x、y父子关系互换
	x->parent = y;
}

3.3 平衡性调整函数

  平衡性调整函数可以说是红黑树里最重要也是最精髓的点，这里不过多解释，待后面记录插入、删除过程时再细细分析。

三、红黑树的空间配置器

  关于红黑树的空间配置器，我只是简单留了个接口，算是有了空间配置器的形式，也方便日后更改(虽然也不大可能会改了 )，就是把new和delete的部分改一下就好。具体如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//rb_tree 空间配置器
template<class Value>
struct _rb_tree_node_allocator
{
	typedef Value value_type;
	typedef value_type* pointer;
	typedef _rb_tree_node<Value> rb_tree_node;
	typedef _rb_tree_node<Value>* link_type;
	//分配内存
	static link_type allocate()
	{
		link_type temp = new rb_tree_node;
		return temp;
	}
	//释放内存
	static void deallocate(link_type p)
	{
		delete p;
	}
};

红黑树结构内相关调用：
	...
	//空间配置器
	typedef _rb_tree_node_allocator<Value> rb_tree_node_allocator;
protected://内存管理相关
	link_type get_node()//获取节点(配置空间)
	{
		return rb_tree_node_allocator::allocate();
	}
	void put_node(link_type p)//释放节点(回收空间)
	{
		rb_tree_node_allocator::deallocate(p);
	}
	...

四、红黑树的迭代器

  上面提到过，STL中完整的红黑树节点是继承红黑树基础节点来完善的。由此，STL中红黑树的迭代器的层次结构也有两层，其中基础迭代器iterator_base对应基础红黑树节点node_base，而完整迭代器iterator则对应完整红黑树节点node。

1. 基础迭代器结构

  先来看基础迭代器结构。在我看来，迭代器就相当于一种封装的指针类型，指向被STL数据结构封装后的一个”节点”。而人们通过操作这个”节点”，就可以遍历整个数据结构，而不用操纵底层的结构。比如在本文的红黑树数据结构中，如果想遍历整个树，就不需要自己声明底层的节点结构类型，而是直接用迭代器就好。
  由上，迭代器中必然有一个底层一些的结构指针来指向可操作的单元，在这个基础迭代器中，这个结构指针就是_rb_tree_node_base::base_ptr，即_rb_tree_node_base*。所以说基础迭代器iterator_base对应基础红黑树节点node_base。
  迭代器最重要的就是”可移动”，即可以指向逻辑上的上一个和下一个，由此需要实现迭代器增加和减少函数。随后还需要重载一些运算符，让迭代器变得好用和方便。由于基础节点中只存在关系并不存在值，所以我们不需要重载*、->、==等操作符，因为它们都涉及到值。由此在这里只需要把重点放到迭代器增加和减少上。
  由于红黑树是二叉排序树，所以一个节点的左子树一定小于等于它，它的右子树一定大于它。按照这个规律，迭代器增加即为：

1
2
3
4
5
1.如果有右子节点，则先向右走，随后向左走到底
2.如果没有右子节点，则上溯父节点
	2.1若当前节点为右子节点，则接着上溯直到不为右子节点
		2.1.1若此时的右子节点不等于此时的父节点，其父节点即为解答
		2.1.2否则直接返回即可(这两个判断主要是防止上溯到根节点)

随后即可找到第一个比它大的节点。
迭代器减少即为：

1
2
3
1.如果是根节点，则右子节点为解答(这个涉及到根节点的设计，以后会分析)
2.如果有左子节点，则先向左走，随后一直向右走
3.如果非根节点也无左子节点，上溯直至当前节点不为左子节点，其父节点即为解答

随后即可找到第一个比它小的节点。
详细代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
//rb_tree 基础迭代器结构定义
struct _rb_tree_iterator_base
{
	typedef _rb_tree_node_base::base_ptr base_ptr;
	base_ptr node;//当前节点
	//迭代器增加
	void increment()
	{
		if (node->right != 0)//如果有右子节点，则先向右走，随后向左走到底
		{
			node = node->right;
			while (node->left != 0)
			{
				node = node->left;
			}
		}
		else//如果没有右子节点，则上溯父节点
		{
			base_ptr y = node->parent;
			while (node == y->right)//若当前节点为右子节点，则接着上溯直到不为右子节点
			{
				node = y;
				y = y->parent;
			}
			if (node->right != y)//若此时的右子节点不等于此时的父节点，其父节点即为解答
			{
				node = y;
			}
		}
	}
	//迭代器减少
	void decrement()
	{
		if (node->color == _rb_tree_red && node->parent->parent == node)//为根节点
		{//若当前节点为红色，且父亲的父亲为自身，则右子节点为解答
			node = node->right;
		}
		else if (node->left != 0)//若有左子节点，则先向左走，随后一直向右走
		{
			base_ptr y = node->left;
			while (y->right != 0)
			{
				y = y->right;
			}
			node = y;
		}
		else//既非根节点也无左子节点
		{
			base_ptr y = node->parent;
			while (node == y->left)//上溯直至当前节点不为左子节点
			{
				node = y;
				y = node->parent;
			}
			node = y;//则父节点即为小值
		}
	}
};

2. 完整迭代器结构

  完整迭代器iterator对应完整红黑树节点node，其中引入了值泛型，所以在完整迭代器中需要进行操作符的重载。由于在之后的使用中，也是操作这个完整迭代器，所以需要定义构造函数。关于重载，重点就是在++和--上，其核心就是调用上面基础迭代器中的增加和减少函数。具体代码如下，非常清晰：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
//rb_tree 迭代器结构定义
template<class Value, class Ref, class Ptr>
struct _rb_tree_iterator : public _rb_tree_iterator_base
{
	typedef Value value_type;
	typedef Ref reference;
	typedef Ptr pointer;
	typedef _rb_tree_iterator<Value, Value&, Value*> iterator;
	typedef _rb_tree_iterator<Value,const Value&,const Value*> const_iterator;
	typedef _rb_tree_iterator<Value, Ref, Ptr> self;
	typedef _rb_tree_node<Value>* link_type;
	//三种构造
	_rb_tree_iterator()
	{

	}
	_rb_tree_iterator(link_type x)
	{
		node = x;
	}
	_rb_tree_iterator(const iterator& it)
	{
		node = it.node;
	}
	//重载操作符
	reference operator*() const//提领
	{
		return link_type(node)->value_field;
	}
	pointer operator->() const//箭头
	{
		return &(operator*());
	}
	bool operator==(const iterator& y) const//==
	{
		return this->node == y.node;
	}
	bool operator!=(const iterator& y) const//!=
	{
		return this->node != y.node;
	}
	self& operator++()//++i
	{
		increment();
		return *this;
	}
	self operator++(int)//i++
	{
		self temp = *this;
		increment();
		return temp;
	}
	self& operator--()//--i
	{
		decrement();
		return *this;
	}
	self operator--(int)//i--
	{
		self temp = *this;
		decrement();
		return temp;
	}
};